Equação quadrática
Equação quadrática ou equação do 2º grau é aquela que se pode reduzir a forma canónica ax2 +bx +c =0.
Onde a ≠ 0, b e c são números reais e recebem o nome de coeficientes e x é a incógnita. São designados por equações do 2º grau porque o maior grau na equação é 2.
Equações quadráticas completas
Todas equações do tipo ax2 +bx +c =0 são chamados de equações quadráticas completas porque possuem valores dos três coeficientes (a, b e c). Conforme se vê o valor de a fica ao lado de x2, o valor de b fica ao lado de x e o valor de c é o valor que não tem a variável x (numero independente).
Dadas as equações abaixo escreva o valor dos coeficientes a, b e c.
a) x2 -10x +25 = 0
a = 1, b = -10, c = 25
b)3x2 -36x +60 = 0
a = 3, b = -36, c = 60
c) -2x 2+ 5x -1= 0
a = -2, b = 5, c = -1
d) X2 + 49 = -14x
X2 + 14x + 49 = 0
a =1, b = 14, c = 49
e) 20 – 5x2 = 4x
-5x2 – 4x + 20 = 0
a = -5, b = -4, c =20
f) 5x -3 = 6 x + x2 + 7
x2 +6x – 5x + 7 + 3 = 0
x2 + x + 10 = 0
a = 1, b = 1, c = 10
g) (-5/3)x2 +(1/2)x + 3/4 =0
a = -5/3 , b = ½ , c = 3/4
Nota: para tirar os coeficiente de a, b e c a equação deve estar na forma canónica ax2 + bx + c = 0. Caso não esteja na forma canónica primeiro devemos organizar a equação
Forma resolvente das equações quadráticas completas
Resolver uma equação quadrática ou equação do segundo grau significa determinar as raízes da equação, ou seja determinar os valores de x que tornam a equação nula (igual a zero), uma vez que a equação e de grau 2 então terá duas raízes, designados por x1 e x2.
Para resolver a equação quadrática devemos seguir os seguintes passos:1 Passo: verificar se a equação esta na forma canónica (ax2 + bx + c = 0), se a equação não estiver na forma canónica deve organizar a equação de modo que fique na forma canónica.
2º Passo: Tirar os coeficientes de a, b e c.
3 passo: Calcular o delta ou discriminante (Δ), onde: Δ = b2 – 4*a*c
4 passo: Calcular as raízes da equação (x1 e x2) Onde :

Observações:
- se Δ > 0 teremos duas raízes distintas (x1≠ x2).
- se Δ = 0 teremos duas raízes iguais ou raiz dupla ( x1 = x2).
- se Δ < 0 a equação não admite raízes reais ou a equação não tem solução em R ( não teremos x1 e x2).
Exemplo:
Determine as raízes da equação: x2 + 7x + 10 = 0
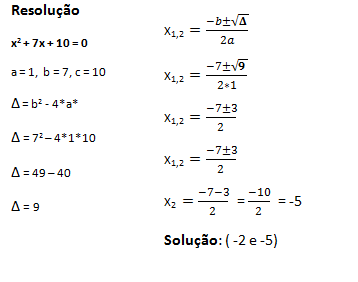
Conteúdo relacionado
- Equações paramétricas
- equações biquadradas
- Equações quadráticas não completas
